Не-белловские квантовые запутанные состояния
Путенихин П.В.
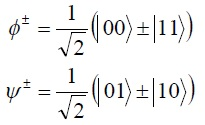
![]()
* * *
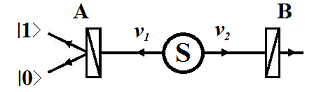
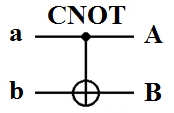
![]() ,
,
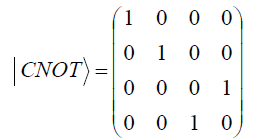
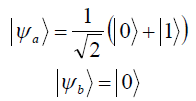
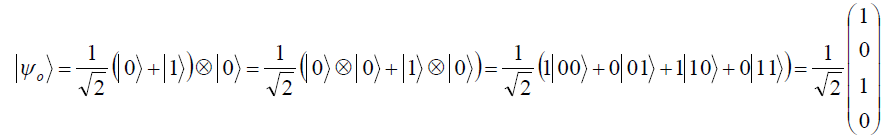
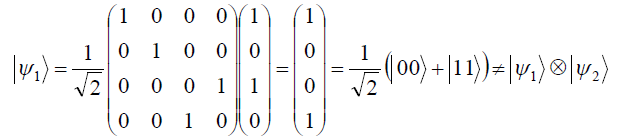
![]()
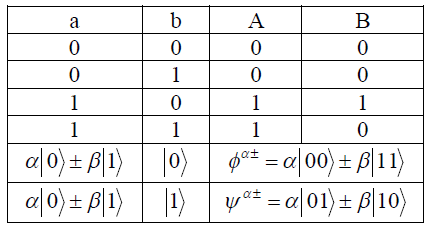
![]()
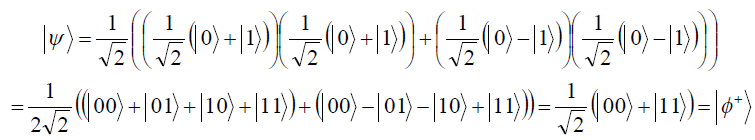
![]()
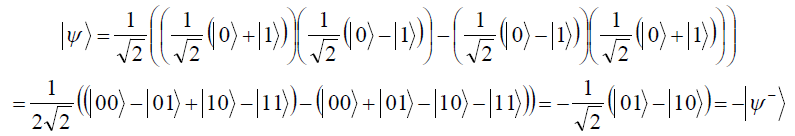
![]()
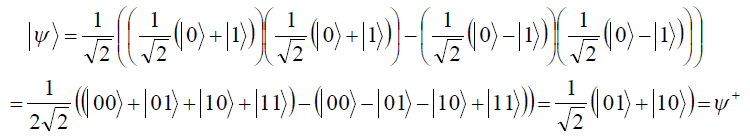
![]()
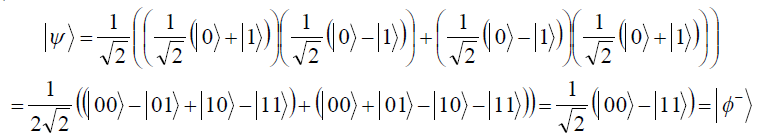
![]()
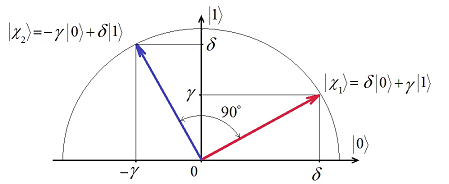
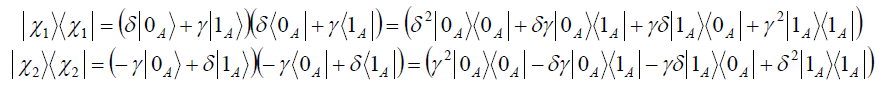
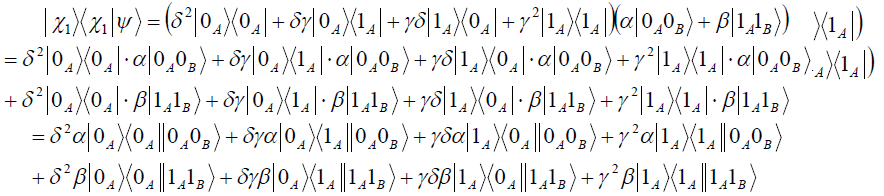
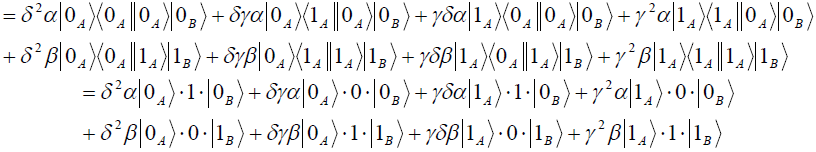
![]()
![]()
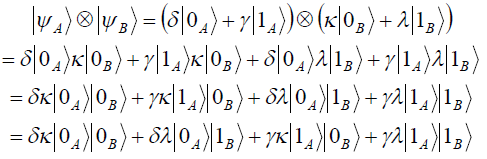
![]()
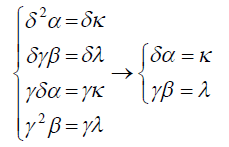
![]()
![]() .
.
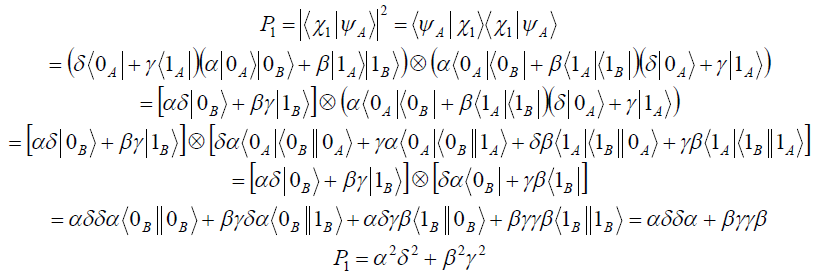
![]()
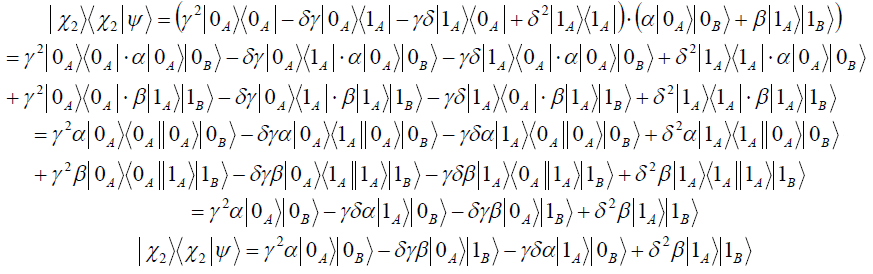
![]()
![]()
![]()
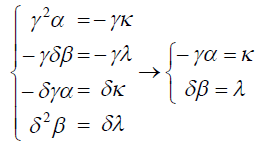
![]()
![]()
.
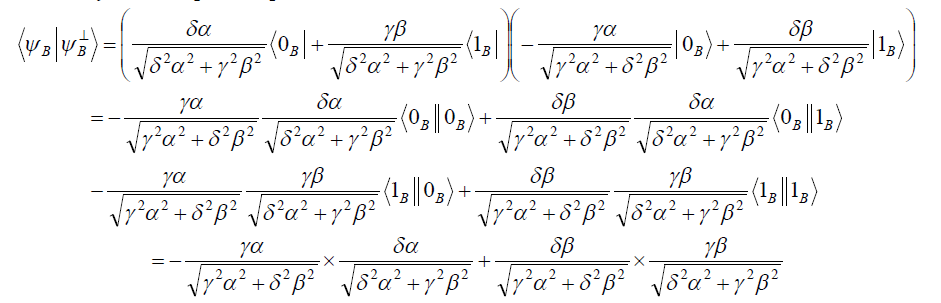
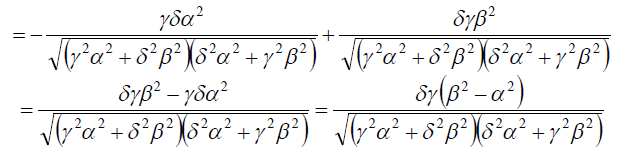
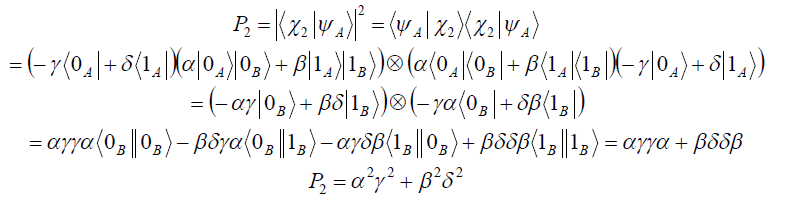
![]()
![]()
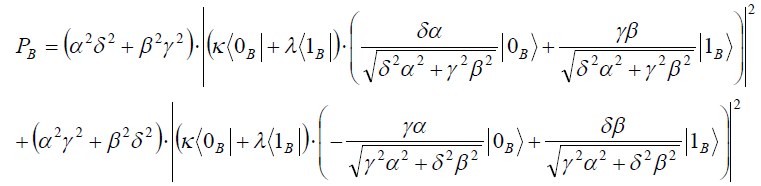
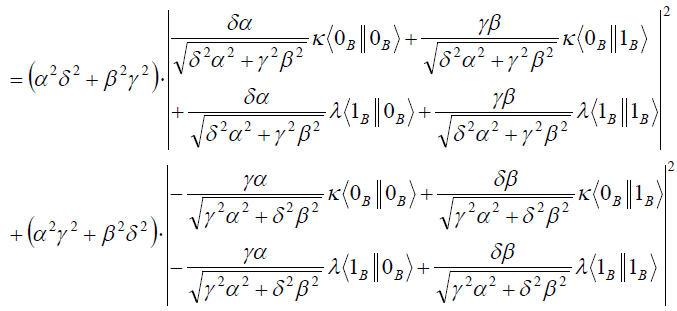
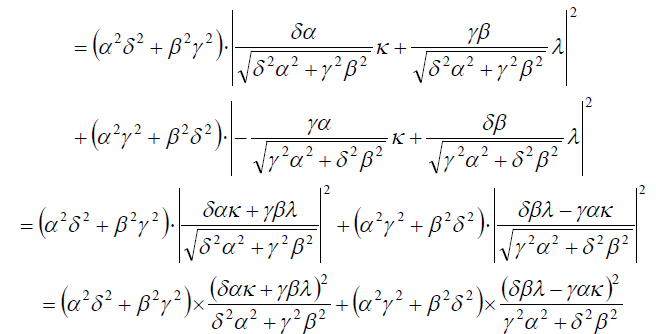
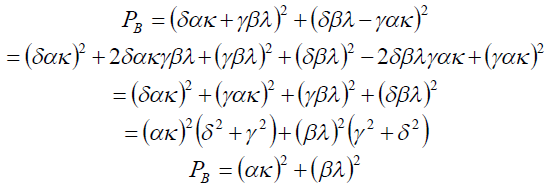
![]()
![]()
![]()
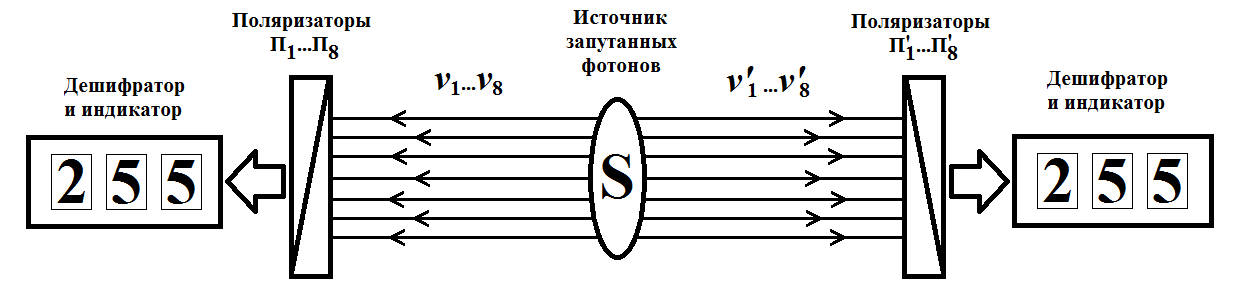
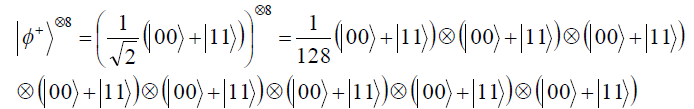
![]()
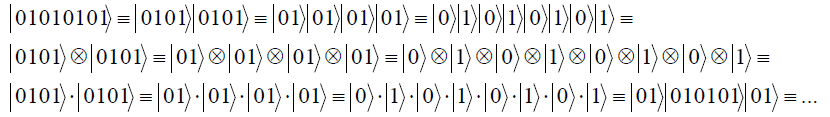
![]()
06.10 - 07.11.2013
Non-Bell quantum entangled states
Poutenikhin P.V.